Дискретное интегрирование
Интегрирование непрерывного сигнала описывается уравнением
Для приближенной реализации интегрирования в дискретной форме имеется ряд алгоритмов. Ограничим класс рассматриваемых алгоритмов дискретного интегрирования алгоритмами, которые можно описать разностным уравнением
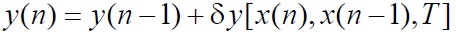 ,
величина приращения на очередном интервале дискретизации, зависящая от применяемого способа интегрирования.
Интегрирование методом прямоугольников
В этом случае величина приращения на шаге n находится как площадь прямоугольника
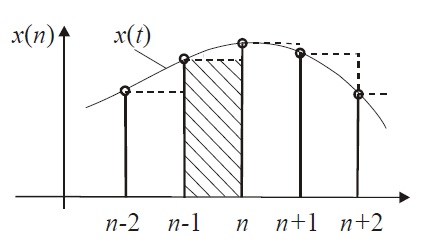
и разностное выражение принимает вид y(n) = y(n-1) + Т*x(n-1).
Здесь: n - номер текущего шага; y(n) - значение интеграла на шаге n; y(n-1) - значение интеграла на предыдущем шаге n-1; x(n-1) - значение подынтегральной функции на предыдущем шаге n-1; T - приращение времени на текущем шаге.
Другими
словами, на каждом этапе работы алгоритма мы прибавляем к уже
накопленной площади, новый прямоугольник. Как видно из графика, на каждом этапе мы теряем некоторую площадь над прямоугольником. Сумма этих площадей является погрешностью. Плюсом данного метода является его простота, а минусом - самая большая погрешностью среди всех описываемых. Интегрирование методом трапецийВ отличии от предыдущего, в данном методе на каждом шаге приращение вычисляется как площадь трапеции, что дает меньшую погрешность: 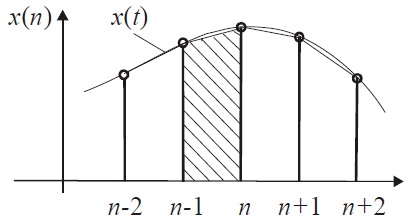 В этом случае разностное выражение будет иметь вид Интегрирование методом параболической аппроксимацииИдея метода состоит в том, что интегрируемая функция x(t) на интервале [(n - 2)T; nT] аппроксимируется параболой по имеющимся трем значениям x(n-2), x(n-1), x(n). Приращение находится интегрированием аппроксимирующей функции на интервале [(n-1)T; nT]. Разностное выражение в этом случае имеет вид
| 
